GOCE gravity field products by means of the space-wise approach (release 5)
The space-wise combined model and the ground level grids
Looking at the grids at satellite level (see the comparisons) it appears evident that lower frequencies and poles can be improved by adding the information provided by other satellites such as GRACE.
To improve the space-wise model a combination of the spherical harmonic coefficients retrieved from the grids with ITSG 2014S has been produced.
Input data:
- Space-wise GOCE spherical harmonic coefficients of the release 5
- ITSG GRACE 2014S spherical harmonic coefficients
- EIGEN 6C4 spherical harmonic coefficients
Processing procedure:
Error standard deviations of the coeffients are used to combine the models. EIGEN 6C4 is used for just the first 3 degrees to correct the very low frequencies obtained after the combination.
In the following figure is it possible to see the influence of the information introduced by the GRACE model, it’s main contribution acts on the degrees below 80 and in the zonal coefficients (that are a direct mapping of the polar ares).
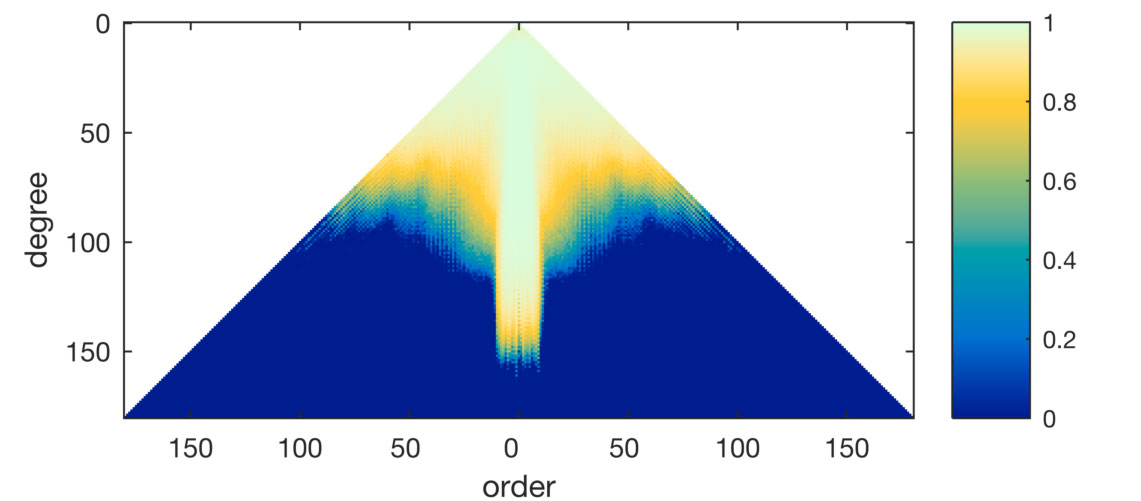
Relative weights for the combination of the coefficients
The errors are computed by propagating the combination to the full error variance-covariance of ITGS and SPW. Propagated error grids are provided together with the data as standard deviations.
Remarks:
- The maximum spherical harmonic degree is 330 because this is the maximum degree used for the modelling of the signal covariance functions in the local collocation gridding.
- The spherical harmonic coefficients with the highest degrees have globally a small signal power, but they could contribute to better model local areas with a high signal-to-noise ratio.
- Any truncation of the spherical harmonic expansion to a maximum degree lower than 330 could introduce errors due to the correlation of the estimated spherical harmonic coefficients.
- The variance-covariance error information of the estimated spherical harmonic coefficients is computed by Monte Carlo simulations, also including the signal omission error up to degree and order 330.
- An error covariance propagation to functionals of the gravitational potential by only using coefficient error variances could be strongly approximated because coefficient error correlations are significant.
Grids comparisons
Space-wise grids (SPWG) can be compared with grids synthesised by spherical other harmonics models.
We provides different comparisons to show pros and cons of the space-wise solution.
All the syntheses are computed at the maximum degree of 330, when a model is truncated at lower maximum degree coefficients are filled with zeros.
References:
- Computation and assessment of the fifth release of the GOCE-only space-wise solution
A. Gatti, M. Reguzzoni, F. Migliaccio, F. Sansò
Presented at the 1st Joint Commission 2 and IGFS Meeting, 19-23 September 2016, Thessaloniki, Greece - GOCE-only grids and spherical harmonic models by the space-wise approach from the full-mission dataset
A. Gatti, M. Reguzzoni, F. Migliaccio, F. Sansò
– in preparation - Optimal multi-step collocation: application to the space-wise approach for GOCE data analysis
M. Reguzzoni, N. Tselfes
Journal of Geodesy, January 2009, Volume 83, Issue 1, pp. 13-29
← go back to the Space-wise GOCE products main page